![]()
FTA解析 故障の木解析
FTA解析とは、予防すべき重大事故(トップ事象)を要因事象に展開し、末端の要因事象(=基本事象)の頻度・確率データからトップ事象の頻度・確率を論理記号に従って計算するという、ベル研究所由来の手法をいう(次のFT図は最も単純なケース)。
FTA解析では、重大事故が一般に多数の要因事象に展開され、それらの一部について頻度見積りができないために全体として使えなくなることが多い。
しかし、ポカヨケ(ヒューマンエラー対策)として、論理記号の「ANDゲート」のみを使う簡単・有益な使い方がある。このページで、これに焦点を当てて「使えるFTA」を事例を介して説明する。
なお、FTA解析を「機械の故障原因の分析手法」と説くのは誤りである。
→ 原因分析は偽物
|
1.FTA解析の概要 2.FTA解析の手順 3.疑似冗長の原理 4.論理記号 5.基本事象 |
6.頻度の表現 7.頻度の見積り 8.ヒューマンエラー 9.FTA解析事例 |
1.FTA解析の概要
以下、FTA解析の概要について説明する。
|
1-1.目的 1-2.効用 1-3.ベル研究所 |
1-4.原因分析は偽物 1-5.使われない原因 |
FTA解析(故障の木解析)では、トップ事象を下図のようなFT図を用いて要因事象に展開し、末端の要因事象(基本事象)の頻度(又は、確率)を見積り、これを集計してトップ事象の頻度等を計算する。


1-1.目的
1.起きては困る重大事故(トップ事象)の発生頻度、又は確率を計算する。
2.トップ事象の頻度等を効率的に下げるために対策を講じるべき末端の基本事象を特定する。
1-2.効用
潜在リスクを顕在化し、予防策を効率的に講じることができる。
1-3.ベル研究所
FTA解析はベル研究所が考案した。
米空軍が開発中だった大陸間弾道弾ミニットマンの発射管制システムの信頼性評価に関する研究をベル研究所に委託して研究された。
機器の故障のほか、不良品の混入・ポカミス・外部からの妨害を含めた総合的な発射失敗の確率を把握することを目的とした。
1-4.原因分析は偽物
FTAを「機械等の故障の原因解析に使える」と主張する指導者がいる。
すなわち、数値的な見積もりや論理記号による計算もせず、従ってトップ事象の頻度を計算することもない。
その意図は、事故を要因事象に展開し、各要因事象に異常がないか調査し、「もし異常が見つかればそれが原因だ」とするものであり、それは特性要因図やトラブルシューティングと混同したものであって、ベル研究所由来のFTA解析ではない偽物である。
例えば、下図に示す機械振興協会の指導例が挙げられる。

1-5.使われない原因
FTA解析は、現実にはほとんど使われない。原因は次の通りである。
- 多数の要因事象(基本事象)に展開しても、その一部でも確率・頻度が不明だと全体が崩壊して使えない。
- 製品の故障、およびそれにより発生した事故の原因を分析する手法です~という誤った考え方に惑わされる(特性要因図やトラブルシューティングとの混同)。→ 原因分析は偽物
- FTA解析を、確率・頻度を用いずに「定性的に行う」という考え方に惑わされる(特性要因図との混同)。
ところが、FTA解析には実に優れた使い道がある。このページでは、この実用性を中心に解説する。
2.FTAの手順
FTA解析で作成する展開図を「FT図」と呼ぶが、以下、FT図の作成手順を簡単に説明しよう。
1. 予防すべき重大な事象(トップ事象)をトップに置く。

2. 頻度見積が可能な基本事象(A1~B3)までトップダウンに下方の展開し、
3. 要因事象の間の関係を、論理記号(OR,AND)を介して系統化し、
4. 各基本事象の発生頻度を見積り、
5. 論理記号(OR,AND)に従って集計して、
6. トップ事象の発生頻度を計算する。
7. 「トップ事象の発生頻度を大きくしている展開線」(critical pass)と基本事象を特定し、対策案を検討する。対策案を実施したと仮定し、トップ事象の頻度計算を更新する。
トップ事象の頻度計算が十分に小さくなるまで、これを繰り返す。
8. 現実に対策を講じた後、適切な期間を置いて、基本事象の頻度を実績と照らして更新し、トップ事象の発生頻度も更新する。
3.疑似冗長の原理
「冗長」とは、同一の機能を並列に結合した構造をいい、その一部の機能を失っても残りの機能で補うことにとって安全を維持することを目的とする(4発のエンジンを持つ航空機)
他方、「疑似冗長」とは、異なる機能を並列に結合した構造をいい、これらの機能を合わせて1つの機能を構成することによってヒューマンエラーを防ぐことを目的とする。
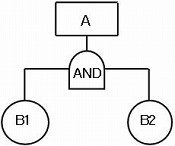
下の図で、起きては困る事象Aを「トップ事象」といい、要因事象B1とB2の両方が同時に起きたときに起きる(=B1とB2をANDゲートで結合)。
事象Aは、最上位にあるから「トップ事象」である。と同時に、下方に要因事象を展開することを予定している意味で、トップ事象は「展開事象」でもある。
展開事象は長方形の枠で囲む。

トップ事象を引き起こす要因事象はB1とB2である。いずれも適切な頻度見積りが可能なので基本事象である。
基本事象は〇で囲む(定義を明確にすれば他の形状の枠でも支障はない)。
基本事象B1とB2のうち、一方が起きてもAは起きない。両方が同時に起きている条件下でAが起きる。この関係を論理記号の1つである「AND」ゲートで表す。
これは、掛け算の関係になる。

B1もB2も「年に1回」ほど起きると予測される事例を考えよう。
1回を1日に置き換えて、起きる日(ブラックデー)が年に1日含まれると考えれば、それらの掛け算がトップ事象の頻度になる。
〔注〕外観不良品の選別作業における見逃しのような、1日に何回も発生するヒューマンエラーには適用できない。
トップ事象の頻度=
これを計算すると次のようになる。

〔注〕1年を260日に置き換えた理由:生活リズムは「活動+睡眠」という1日を最小単位として成り立っている。この最小単位を1枚のカードとみなし、年間260日(=260枚のカード)の中に運の悪い日(ジョーカー)が混入しているものとみなしたもの。
1時間(H)と次の1時間の間には生活リズムの区切りがないので、1時間は生活リズムの単位として扱うことはできない。1週間、1か月も同様である。
この事例では、年間の稼働日を260日とみて、「260年に1回」という結果になるが、この値を十分に小さいとみるか、それでも高いとみるか、それは事の重大性によりけりで、ケースによって異なる。
製造業で不良品が流出するというトップ事象なら、「260年に1回」は十分に小さいとみるべきだし、旅客機の墜落に繋がる事例や新幹線の脱線転覆につながる事例なら対策不十分とみるべきである。
4.論理記号
主に使用される論理記号を下の一覧表を示す。

〔注〕
1. 上の表は原則的なものであって、支障がなければ異なった記号を用いてもよい。例えば、基本事象を〇で囲むことが不便なら、それと分かる形で展開事象と同じ□枠で囲ってもよい。
2. "AND" ゲートや "OR" ゲートは、記号の中に "AND" や "OR" を記入した方が理解しやすい。
5.基本事象
基本事象は、システムを構成する末端を意味するのではなく、「適切な頻度見積が可能な末端」の意味である。従って、必ずしも最後まで展開する必要性はない。
|
5-1. 製品の故障 5-2. 人の行動 |
5-1.製品の故障
基本事象は、トップ事象から始まって何段階かの中間事象を経由して(中間事象を経由しない場合もある)到達する展開の端末に位置する事象であり、「頻度を見積もる事象」である。
しかし、どこまで展開して頻度を見積もるのが適切か、ケース・バイ・ケースである。
利用者による展開
例えば、会社員が顧客企業で開かれる重要な会議に遅刻するとか、持参したPCが故障するとかの不運によって対応に失敗する頻度を計算しよう(他にも基本事象はあり得るが、ここでは省略する)。

PCの利用者が故障頻度を評価する場合は、単に、経験上知られている故障頻度(1回/5年)を適用すればよい。また、電車の利用者が電車の遅延頻度を評価するには、単に、経験上知られている遅延頻度(1回/月)を適用すればよい。
なぜなら、利用者は細部に展開できないし、仮に展開しても改善策を打てる訳でもなく、現実の頻度を受け入れるしかないからである。
管理者による展開
PCのメーカーがPCの改良のために故障頻度を評価する場合は、全ての要因事象(全ての部品の故障)に展開する必要がある。さもないと、改良すべき部品が特定しないからである。
5-2.人の行動
ある作業のヒューマンエラーを防止するため、その作業を複数の作業要素に展開して分担を分け、各作業要素を基本事象とすることができる。
〔参照〕
→ 組付けミスのFT図
6.頻度・確率の表現
実務では、頻度を使用することが多いと思うが、確率を扱うこともできる。
「年に1回」ほど発生すると見込まれる場合、それが特定の日に起きる確率は 1/365(工場の稼働日なら 1/260 である。また、特定の月に起きる確率は 1/12 である。
頻度と確率の表し方を整理すると、下の表のようになる。
| 事象の頻度 | 頻度表現 | 確率表現 |
|---|---|---|
| 年に1回 | 1回/年 | 1/260 |
| 月に1回 | 12回/年 | 1/22 |
「年に1回」は、260日(稼働日)のうちの1日がブラックデーになると考えて「1/260」と表すことができる。ただし、病院や消防署のように年中無休の職場は「1/365」に修正する必要がある。
合否判断に明確な基準はないが、多数人の生命に関わるような大事故なら「1万年に1回」程よりも小さい頻度が求められる。
本件の場合のような個人的なケースで少額の損失を問題とする場合は、「10年に1回」程ほどで十分かと思われる。
7.頻度・確率の見積
FTAを実施して遭遇する問題点と対策を紹介する。
|
7-1.問題点 7-2.頻度見積法 ・中間法 ・信用法 ・平均法 ・集積法 ・修正法 ・みなし法 |
7-1.FTAの問題点
FTA解析を実施するには、次の事項を習得する必要がある。
- FT図の作り方
- 論理記号の設置
- 基本事象の頻度見積り
- トップ事象の頻度計算
しかし、これらを習得しても、事実上はFTA解析を使えないという問題がある。実は、FTA解析手法を使う人はほとんどいない。なぜか?
必要なデータが手元にないため、「基本事象の頻度の見積り」が困難だからである。例えば8個の基本事象のうち、7個の見積りができても1個だけ頻度が分からなければ、それでFTA解析は頓挫する。
考案者であるベル研究所は、過去の故障や事故の膨大なデータを入手できた。それ故に、頻度計算が可能であったと推測される。
しかし、一般の企業でFTA解析を実施しようとやたらと細部まで展開しても、その頻度データがないケースが大半を占め、実施が困難である。そのような事情で、FTA解析はどのような事故の頻度予測にも使える訳ではない。しかし、工夫によってうまく使えば、非常に便利で有効な手法になる。
7-2.いろいろな頻度の見積法
基本事象の頻度(確率)見積を正確に行うには、現実の頻度データが必要である(データでモノを言え)。
しかし、そのデータを入手できないケースが多いのが現実である。そこで、このページでは、「データでモノを言う」に近い基本事象の頻度(確率)見積の仕方を紹介する。
・中間法
「10年に1回」より明らかに多く、「月に1回」より明らかに少ない事象は、「年に1回」と見積もる。
「年に3回」や「月に2回」~というような見積りは、後日、実績データが得られた後に修正法によって行う。
〔注〕上の式で、分母と分子の次元が異なることが気になる人は、分子の単位を「日」に読み替えるものとする。
・信用法
信用できるメーカー製品のセンサーの場合、メーカー保証が5年の場合に「5年とみなす」ことによって安全に定期交換の保全を行う。
〔注〕定期点検と定期交換
「定期点検」では異常がなければ放置し、異常品のみを交換する。これに対し「定期交換」では、点検の結果を記録し、異常の有無に関わらず交換する。
・平均法
人が犯すヒューマンエラー(ポカミス、うっかりミス)の頻度は正確には分からないし、人によって大きく異なり、同一人でも日によって変化する。
しかし、「年に1回」と見積もって支障がないことは経験から分かっている。このように経験上、平均的に予測される頻度を適用することを「平均法」と呼んでいる。
同様に、機械の故障も「年に1回」と見積もって支障がない場合が多い。ただし、経験や情報から5年に1回程度と分かっている場合は、そのデータが優先する。
・集積法
パソコンの故障頻度を求めるには、本来、パソコンを構成する膨大な部品・コンポーネントに展開しなければならない。
しかし、常にそうとも言えず、パソコン(市販の完成品)の故障頻度を「年に1回」と見積ることもできる。
〔参照〕→ 製品の故障
・修正法
FTAを適用した後、数年間の実績を見て基本事象の見積を変更する。最初「年に1回」と見積もった機械が4年後も異常がなければ、整備をしてから「2年に1回」と修正する。
・みなし法(擬制法)
事故を起こす事象であることに違いはないが、次の事象は無視して起きないものとみなす。
- 対策費用が高すぎる基本事象
- 対策の方法がない基本事象
- トップ事象よりも被害大の基本事象
トップ事象を展開すると、基本事象に見積り不能なものが登場することがある。下図は風力発電機の回転翼の破損をトップ事象にして展開したものであるが、頻度見積りが困難な様々な基本事象が列挙された。

一番下に並ぶ基本事象のうち、「鳥の衝突」と「台風」による破損は日本で現実に発生している。これら基本事に対する頻度見積もりの筆者案を下の表に示す。
| 基本事象 | 見積り |
| 台風 | 無視 |
| ヒョウ | 無視 |
| 竜巻 | 無視 |
| 巨大地震 | 無視 |
| 巨大津波 | 無視 |
| 火山石 | 無視 |
| ヘリ・航空機の墜落 | 無視 |
| 渡り鳥の衝突 | 1/10年 |
| 隕石の落下 | 無視 |
| 人工衛星の落下 | 無視 |
| ロケット・ミサイル | 無視 |
最初に掲げた「台風」
過去に経験した台風の最大風速に耐える設計なので、これを超える台風が来ても対策費が高すぎて対応できず、「無視」とする。
破損が起きてもやむを得ないという意味である。
「ヒョウ」と「竜巻」
回転翼が破損するような大規模なものが発生するとは思われないが、発生しても対策費が高いので「無視」する。
下の方にある「渡り鳥の衝突」
実際に日本でも地域によって発生している。対策費は回転翼よりも低く押せられるので「10年に1回」とした。
地域によっては対策を要することになる。
その他の「無視」する事象
これらが起きれば、もはや風力発電機の回転翼どころの話ではなくなる。回転翼などはどうでもよいから、人身被害が生じないように避難することに専念すべし、である。従って、これらは考慮しない(対策もしない)ものとする。
8.ヒューマンエラー
「ヒューマンエラー"humam error"」とは、人間が犯す過ち、思い違い、勘違い、亡失、疲労、発作等が原因になって起こす過ち~である(日本規格協会:TQC辞典)。俗にいう「ポカ、うっかり」と同義である。
以下、このヒューマンエラーに対してFTA解析が有効と思われる事例を紹介する。
|
8-1.誤った理解
ヒューマンエラーについて「なぜ、起きたか?」を繰り返す誤った「なぜなぜ分析」を指導する者もいるが、それは「人はポカをするように出来ている」という事実を無視した考え方である。
人がうっかりするのは、長い進化の過程で獲得した「人の本来の姿」であって、原因がある訳ではない。強いて原因を問うなら何か脳のどこかに異常が起きたに違いない。特効薬や脳手術を考えようにも、そのよう医療は普及していない。故に、原因を問うことは厳禁である。
従って、「うっかり」に対しては、次のいずれかの対策を講ずる以外にない。
- 発生対策:発生を自動的に予防する対策
- 影響対策:発生しても、影響を回避・軽減する対策
- 検知対策:大事に至る前に検知させる対策
いずれもハードウェアとソフトウェアがあり得るが、FTA解析をソフトウェア的な発生対策に利用することができる。
8-2.冷凍梱包の事例
「疑似冗長設計」によって思い込みによる「うっかりミス」の対策を講じた事例を示そう。
|
ある工場の出荷作業で、通常梱包と冷凍梱包を行っており、冷凍梱包には温度記録計を同梱する決まりがある。梱包の中身は作業者が確認して写真を撮影することに決められていた。 ある日、作業者がうっかりして冷凍梱包に温度記録計を入れ忘れ、そのまま10台の製品が出荷されてクレームになった。 作業者に対する指示は伝票で正しく行われ、梱包の中身も写真撮影されていたが、確認が抜けていた。 |
〔解説〕
このケースでは、作業者が伝票の指示を受けて冷凍梱包をしたが、温度記録計を失念した。温度記録計を同梱しないのが正常だと思い込んでいるから、写真撮影も確認も対策にならない。
温度記録計を思い出させる対策が必要なのである。
そこで「冷凍梱包が正しい」ことを気づかせる、FTA解析による疑似冗長設計を検討する。
1. 伝票を色分けして、通常梱包は白色、冷凍梱包は青色の用紙を使う。
作業者B1と出荷担当者B2に青色の伝票を回しておく。
2. 作業者B1が温度記録計の梱包を担当し、出荷担当者B2が温度記録計の準備を担当する。

3. B1が温度記録計を取りに行かないとB2が異常に気づき、B2が準備を忘れるとB1が異常に気づく。
4. B1、B2のそれぞれが忘れるのは「年に1回」程度と思われるが、これが「260年に1回」に改善される。
これによって仕事量は増加しない(仕事の配分の変化があるのみ)。むしろ、従来B1が行うものとされた写真撮影などの点検作業が減る。
8-3. 疑似冗長と二重点検
疑似冗長と二重点検の違いを正確に理解しよう。
1. 二重点検
2名で同じ点検を重複させる「二重点検」を考え勝ちであるが、これには問題がある。
1. 点検作業は何ら付加価値を生まないから、いたずらに点検作業を増やすと、工数の増加をもたらす。
2. 二名で同じ点検をすると、「自分が忘れても相手がやってくれる」という油断を生む。
〔事例〕→ 2000年6月から7月にかけて発生した雪印乳業の食中毒事件で、大樹工場では当時3人の検査員が大腸菌の検査を担当し3人とも手抜きをしたと報道されている。
2. 疑似冗長

冗長設計では同一機能を並列に配置する(例:複数のエンジンを有する航空機)。
これに対して、1つの機能を複数に分割して(従って、異なる機能を)並列に配置することを「疑似冗長設計」という。
ヒューマンエラー対策として、仕事量を増やさず、しかも付加価値のない点検作業を排除することができる(ただし、点検作業そのものを分割して疑似冗長設計とする場合を除く)。
以上のようなFTA解析を利用したヒューマンエラー対策を単なるダブルチェック(二重点検)ではないかと誤解する人を見受ける。しかし、それは全く違う。
| 二重点検 | 疑似冗長設計 |
| 2名が同じ点検 | 各別の作業を分担 |
| 作業と人員が増える | 分担を変えるだけ |
| ミスが誰にも見えず → 思い込みに無効 |
ミスが相方に見える → 思い込みに有効 |
8-4.組付けミスの事例
|
ある工場で作業者がブラケットの組付けを忘れ、そのまま完成品が出荷されてクレームになった。 従来、数種類の部品を組忘れないための対策として「先に必要な部品を取り揃える」という自己ピッキングを行う決まりになっていた。 しかしこの作業者は「自分は組忘れや部品違いを起こさない」という思い込みがあって、規則を守らなかった。 〔担当部署の反省点〕 |
〔解説〕注意事項をポイントカードに記載するのが流行した時代があった(西暦1900年~2000年)。「ワンポイント・レッスン」と呼ぶ場合もある。
トラブルが発生するたびにポイントカードを掲示し、職場中がポイントカードで埋め尽くされ、誰も読む者がいないという体裁主義が横行した。ポイントカードで対策が完了したものとされ、その結果、トラブルは一向に解消しなかった。職場から一切の掲示を除去する運動が始まり、その結果「スッキリしてトラブルが減った」との感想が多かった。
本件に疑似冗長設計を適用すると、次のようになる。

1. ピッキングと組付け作業の担当者を分ける。作業量は増やさず、作業の分担を変更するだけにする。
2. ピッキング作業者B1に異常があれば組付け作業者B2が組み付けできずに異常に気づく。
3. B2が組付け漏れをするとB1が(容器に部品が残っているという)異常に気づく。
4. その結果、365年に1回(稼働日が260日なら、260年に1回)程度になる。
8-5.患者の受け渡し
|
ある病院で、手術室に別の患者が連れてこられ、危うく間違った手術が行われそうになったので、対策を講じたい。 |
〔解説〕
患者を連れて来た看護師Aと手術室の看護師Bか患者Cの目の前で「受け渡し確認」を行う(疑似冗長設計)。
A:患者氏名は、佐藤明美さんです。
右目の白内障の手術です。
B:はい、確認しました。
生年月日は昭和45年3月9日、IDは432765 ですね。
A:はい、確認しました。よろしくお願いします。
さらに、相手が正常に点検したことの証として、患者確認書に両者が押印し、執刀医に手渡し、執刀医が確認する。いずれか一人で患者を手術室に連れてくる事態を防ぐためである。
A、B いずれもミスをするのが年に1回と見積もって、両者が同時にミスをするのは、365年に1回に削減することができる。
365年に1回の頻度は、事実上、発生しないと言えるレベルである。

8-6.総クレーム件数の低減
|
その工場の昨年度のクレームは冷凍梱包の温度記録計の入れ忘れが2件、ブラケットの取り付けもれが3件、合計で5件であった。 クレームの合計件数の削減を図りたい。 |
〔解説〕
事例(1)と事例(2)を合計したものがトップ事象の「年間クレーム件数」になるから、ORゲートで結合する。
参照 → 論理記号
これらは「トップ事象」の下位にある展開事象であり、「中間事象」という。

事例(1)が2件、事例(2)が3件発生したものとして対策後の頻度を加算すれば、クレームの発生は「50年に1回」となる(下図)。

多数の経路で構成される場合は、最も頻度の高い経路(クリティカル・パス)に重点的に対策を講じる。
9.当研究所のFTA解析事例
当研究所が現に実施している有効なFTA事例を紹介する。
|
|
セミナー当日に何らかの事情でセミナーを開催できない事態が発生すると、受講者の皆様に多大なご迷惑をおかけすることになる。 受講者は仕事を休み、中には航空機やホテルを利用される方もおられ、講習会場に来てみると中止というのでは当研究所の言い訳が立たない。 そこで、せめて当研究所の怠慢で中止になる事態だけは何としても回避すべくFTA解析を行った。 |
〔解説〕
・トップ事象=「受講者の方々に連絡なしにセミナーを中止する事態」である。
ただし、連絡する時間もない急病、交通事故、地震等の災害は、不可抗力によるものとして対象から外す。
・講習会が中止になる要因事象はいろいろあり得るので、想定外が発生しないよう「総枠設定」を行う。本件の場合は5Mを利用して総枠を設定するのが最適である。
9-1.総枠の設定
下の図で、中間事象として5Mを列挙し、それぞれの基本事象象に展開する。

〔参照〕 → 論理記号
このように、展開すべき要因事象の抜けを防ぐために「これ以外にはあり得ない」という総枠を設定して、その中で要因事象を列挙する。
要因事象が全て分かっている場合は、総枠設定は不要である。本件では総枠として5Mを使っているが、これに限らない。
参照: 5Mとは、→ 工程の構造
9-2.頻度の見積
本件の場合、下図のように見積もることができる。

何も対策をしないと、上図に示すように危険な日(ブラックデー)は年間で17日あることが分かる。
他方、講習会は年に6回開催する(6日/年)。すると、ブラックデーと開催日がかち合う頻度は、次のようになる。

「2年に1回」ほど危ない目に合う計算になり、勿論、不合格である。

9-3.対策と効果
そこで、本件の対策を考えたものが次の図。

1. 列車異常の対策は、会場に近いホテルに前泊して徒歩で講習会場に行くようにする。これで頻度=0 になる。
2. PC、アダプター(電源)、マウス、プロジェクターは予備品を会場に持ち込み、故障したら直ちに交換する(待機冗長設計)。
〔注〕冗長設計とは
エンジンが4個ついた航空機は、何らかの事情で3個が故障しても、1個だけ正常であれば着陸することができる。このように、本来は不要な、同じ働きをする要素を余分に装備する仕組みを「冗長設計」という。
その余分な要素を常に使用する「常用冗長設計」、普段は使わない「予備品冗長設計」、簡単に切り替えられる「待機冗長設計」がある。
頻度計算は、いずれも自乗する。

これが4個あるから4倍する。
 -----(1)
-----(1)
3) 講師の急病については、事務局が受講者の方に緊急電話を掛けるものとする。担当する事務局にも支障が生じることが「年に1回」あり得るとする。
 -----(2)
-----(2)
* 停電は災害がない限り、日本では1回/10年程度であり、これに自家発電設備を有する会場を使うという対策を織り込む。
以上の(1),(2),(3)を合計する。

上の計算を下の図に示す。

ブラックデーは 1日/50年であり、開催は6日/年予定するとして、これらがかち合うのは下図のように掛け算になる。

FTAにより、リスク全体を見渡し、クリティカル・パス(最大リスク経路)が可視化される。
9-4.実績による修正
このような概算見積もり下で5年過ごした 実績データ と照合して、頻度見積を修正した。
パソコン等の故障や講師の病気などを、「1回/年 → 1回/4年」に修正した結果、図のようにトップ事象の頻度は、さらに小さいものとなった。
